Some context on spaces and tangent spaces can also be found on here.

Robotics state estimation is basically calculus on curved surfaces.
The set of rotation matrices $SO(3)$ and rigid transforms $SE(3)$ are Groups, not Vector Spaces.

• $R_1+R_2$ is NOT a rotation matrix.
• You cannot take a derivative directly on the matrix.

The Manifold and The Tangent Space

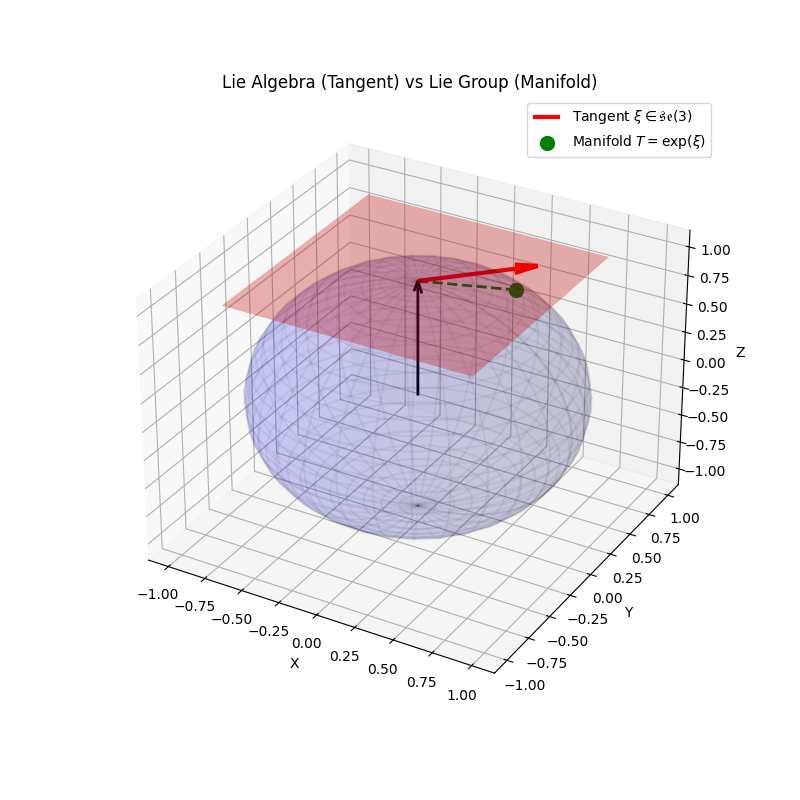
Imagine a sphere (Manifold $\mathcal{M}$). If you stand on the north pole, the flat plane touching your feet is the Tangent Space ($T_x\mathcal{M}$).

• Manifold: $SE(3)$. Curved, 4x4 matrices.
• Tangent Space: $\mathfrak{se}(3)$. Flat, 6x1 vectors.

We do optimization (adding $\mathrm{\Delta }x$) in the flat Tangent Space, then project back to the Manifold.

The Maps

1. Hat Operator $(\cdot {)}^{\wedge }$:
   Converts 6x1 vector $\xi$ to 4x4 matrix representation.

2. Exponential Map ($\exp$):
   Projects tangent vector onto the manifold.

Physically: If you move with constant velocity twist $\xi$ for 1 second, you end up at pose $T$.

3. Logarithm Map ($\ln$):
   Projects manifold element back to tangent space.

The "Box Plus" Operator ($⊞$)

Since we can't do $T+\delta$, we define a generalized addition.
There are two conventions. Stick to one!!! I prefer the Right Multiplication convention (used in g2o, GTSAM).

This means: "Start at frame T, then apply a small local perturbation $\xi$ in T's frame."

The Adjoint (${\text{Ad}}_T$)

Sometimes you have a twist defined in the World frame, but you need to apply it in the Body frame. The Adjoint map transforms tangent vectors between coordinate frames.

For $SE(3)$:

Jacobians on Lie Groups

When we linearize measurement functions, we need the derivative with respect to the Lie Algebra perturbation.

We treat $\xi$ as a small perturbation near 0.

Typical Jacobians you will see:

1. Rotation of a point: $\frac{\partial (Rp)}{\partial \varphi }=-[Rp{]}_{\times }$
2. Inverse pose: $\frac{\partial (T^{-1})}{\partial T}=-A{d}_{T^{-1}}$