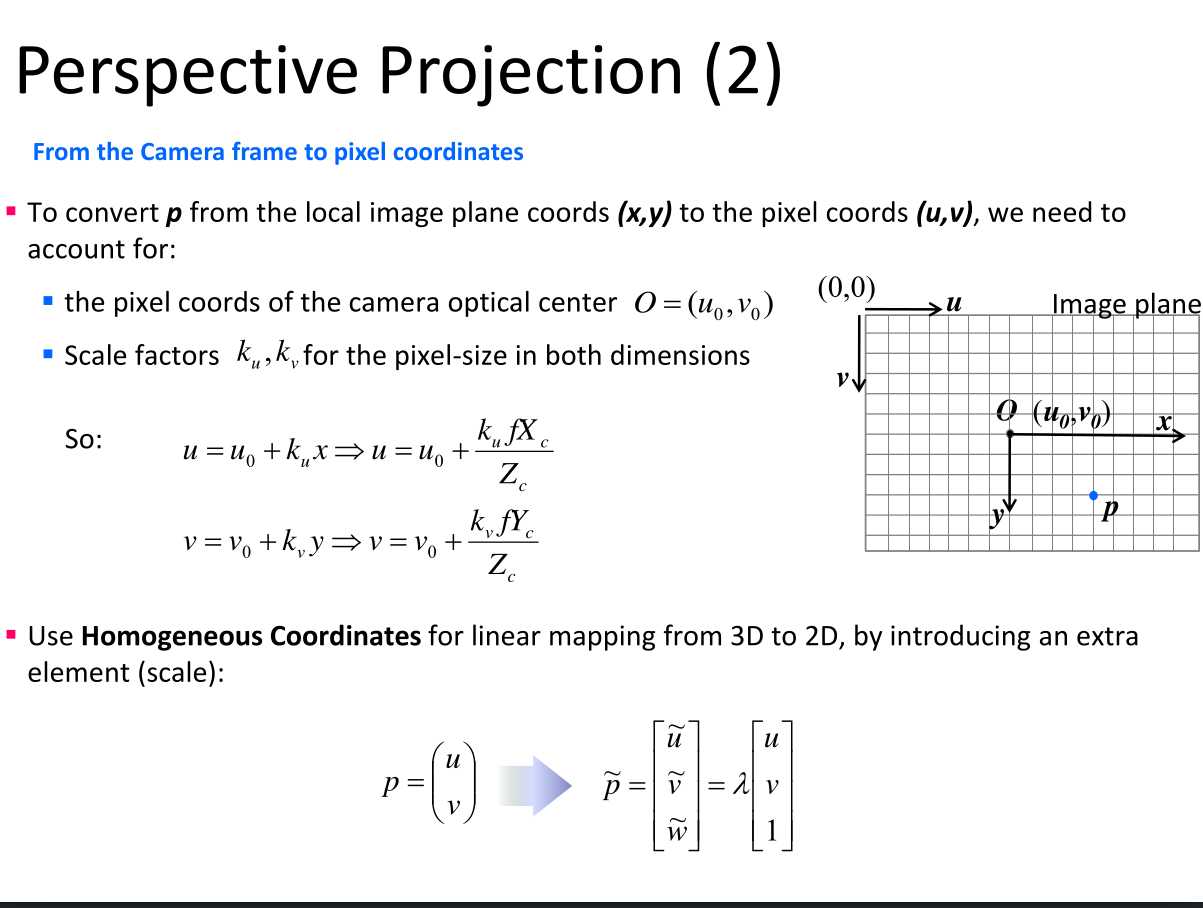
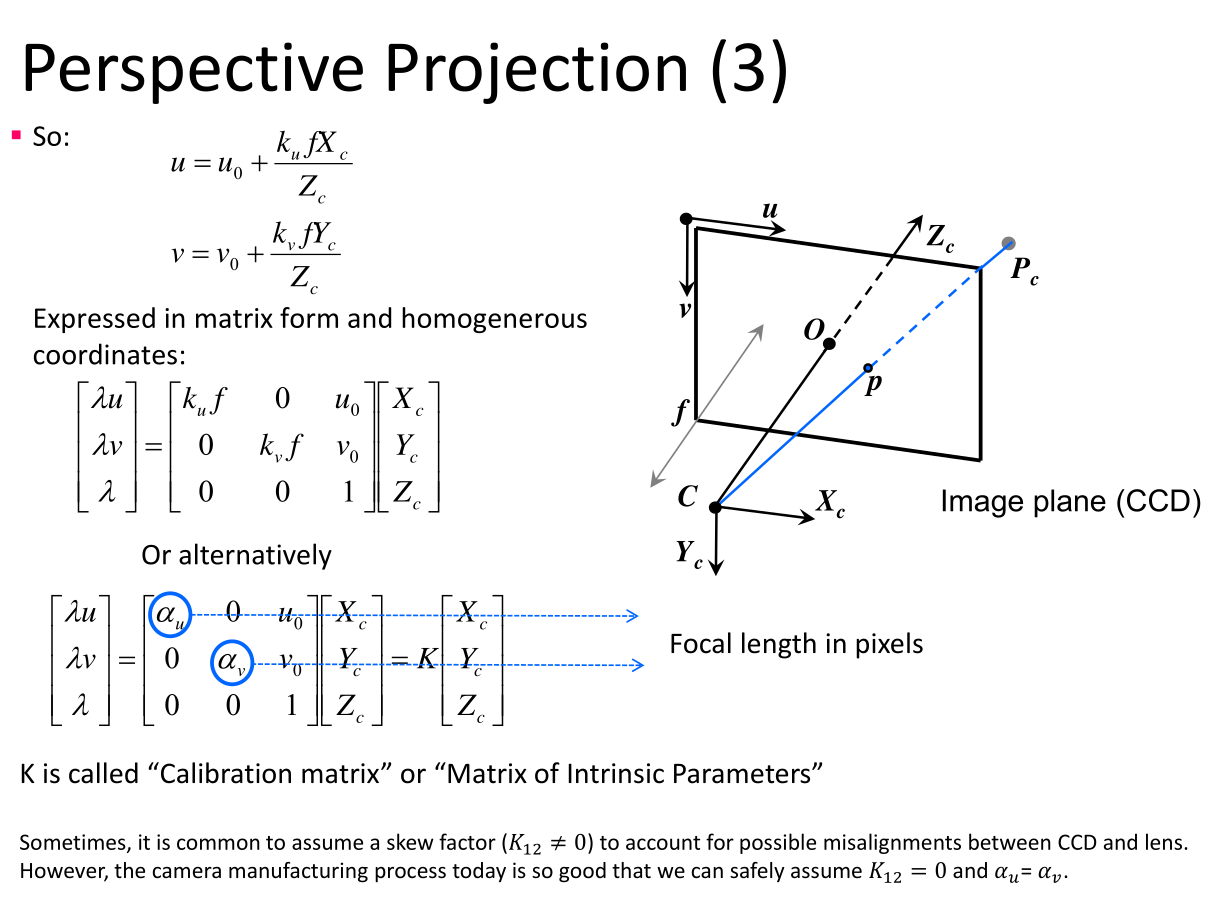
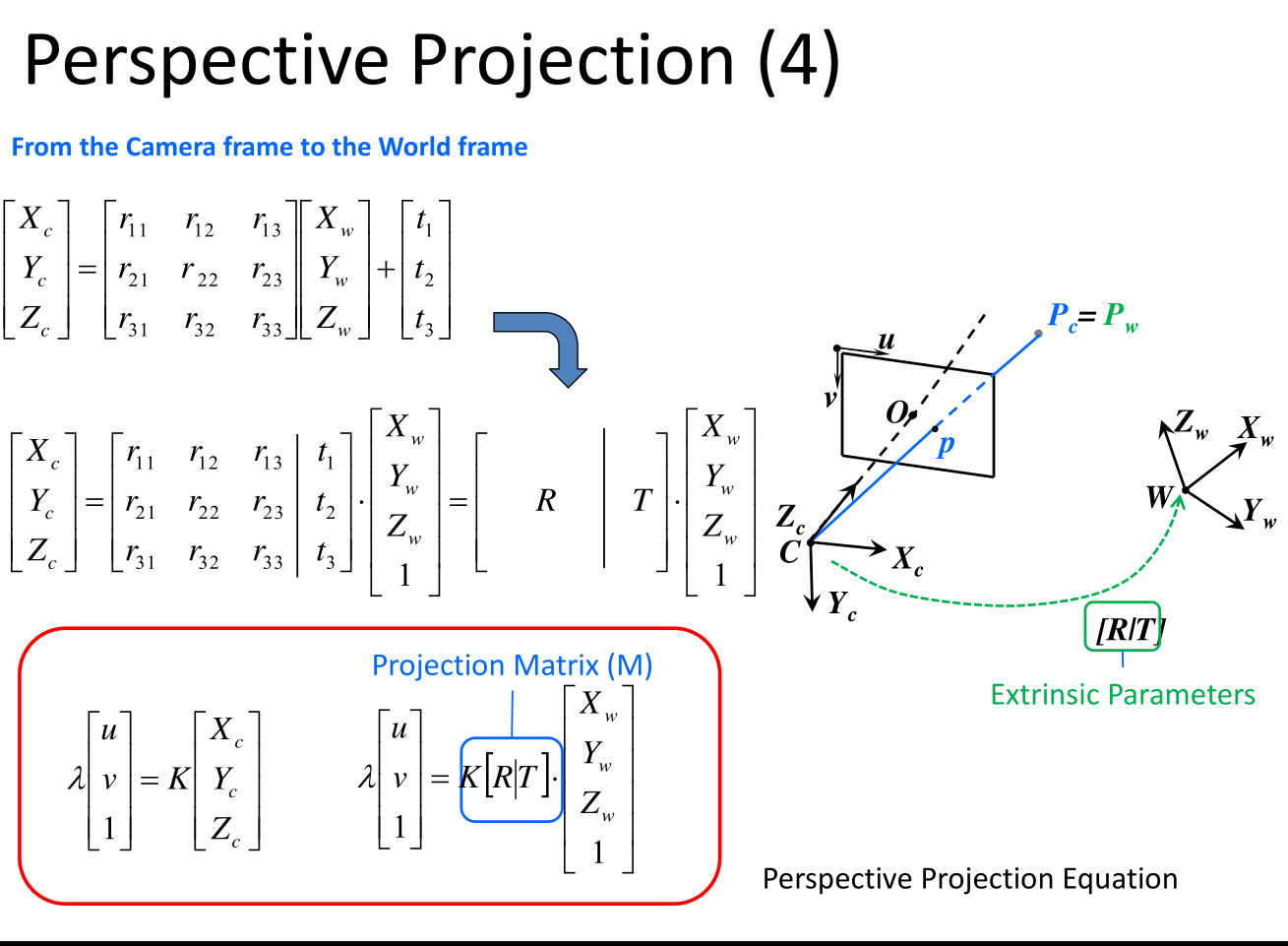
Perspective Projection

Pasted image 20251121180231.png
Pasted image 20251121180243.png
Pasted image 20251121180255.png

Q) Determine K for a digital camera with Image Size 640 x 480 and horizontal field of view equal to $90^{\circ}$ , assume principal point in the center of image and squared pixels. What if fov?

So because principal point is in center $c_{x} = \frac{640}{2} = 320$ and and $c_{y} = \frac{480}{2} = 240$ .
And because of:
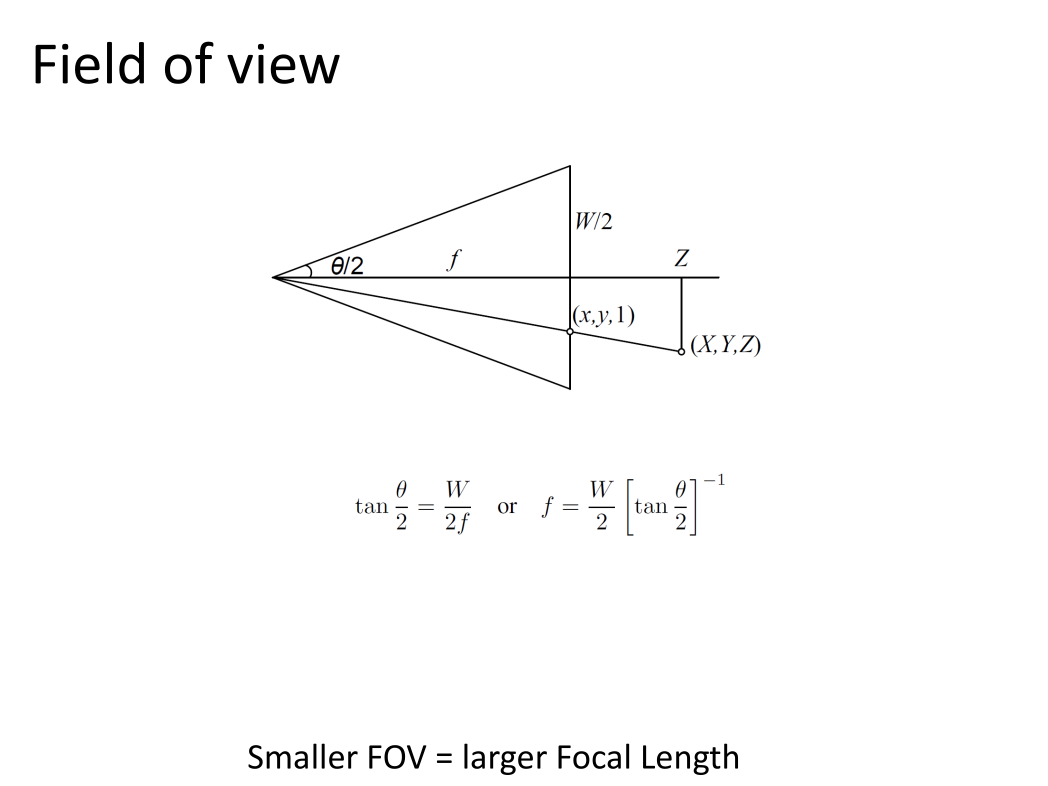
We also have that $f_{x} = f_{y} = f$ because of squared pixels.
$t a n (\frac{90}{2}) = \frac{W}{2 f}$ , so $f = \frac{W}{2 t a n (45)} = \frac{640}{2} = 320$
Vertical fov can be calculated as: ${f o v}_{v} = 2 t a n^{- 1} (\frac{H}{2 f}) = 2 t a n^{- 1} (\frac{480}{640}) \approx {73.74}^{\circ}$

The Proof: Why Parallel Lines Meet

To Prove: Show that two parallel lines in the 3D world project to lines in the image that intersect at a single specific pixel (the Vanishing Point

Define Parallel Lines in 3D
Two lines are parallel if they have the same direction vector but different starting points.
Let's define the direction vector as $\vec{V} = [l, m, n]$ .

Line A: Starts at point $A_{0} = (X_{a}, Y_{a}, Z_{a})$ .
Equation: $[\begin{matrix} X (s) \\ Y (s) \\ Z (s) \end{matrix}] = [\begin{matrix} X_{a} + s \cdot l \\ Y_{a} + s \cdot m \\ Z_{a} + s \cdot n \end{matrix}]$
Line B: Starts at a different point $B_{0} = (X_{b}, Y_{b}, Z_{b})$ .
Equation: $[\begin{matrix} X (s) \\ Y (s) \\ Z (s) \end{matrix}] = [\begin{matrix} X_{b} + s \cdot l \\ Y_{b} + s \cdot m \\ Z_{b} + s \cdot n \end{matrix}]$

Here, $s$ is the distance parameter. As $s \to \infty$ , we move infinitely far away along the line.

Apply the Camera Projection

Recall the basic pinhole projection equations (assuming standard camera frame where focal length is $f$ ):

u = f \frac{X}{Z}, v = f \frac{Y}{Z}

Let's substitute our line equations into this projection.

For Line A:

u_{A} (s) = f \frac{X_{a} + s \cdot l}{Z_{a} + s \cdot n}

v_{A} (s) = f \frac{Y_{a} + s \cdot m}{Z_{a} + s \cdot n}

For Line B:

u_{B} (s) = f \frac{X_{b} + s \cdot l}{Z_{b} + s \cdot n}

v_{B} (s) = f \frac{Y_{b} + s \cdot m}{Z_{b} + s \cdot n}

Take the Limit (The "Vanishing" part)

For $u_{A}$ :

lim_{s \to \infty} u_{A} (s) = lim_{s \to \infty} f \frac{X_{a} / s + l}{Z_{a} / s + n} = f \frac{0 + l}{0 + n} = f \frac{l}{n}

For $v_{A}$ :

lim_{s \to \infty} v_{A} (s) = lim_{s \to \infty} f \frac{Y_{a} / s + m}{Z_{a} / s + n} = f \frac{0 + m}{0 + n} = f \frac{m}{n}

same for Line B:

lim_{s \to \infty} u_{B} (s) = f \frac{l}{n}

lim_{s \to \infty} v_{B} (s) = f \frac{m}{n}

Both lines converge to the exact same pixel coordinate:

p_{\infty} = (f \frac{l}{n}, f \frac{m}{n})

This point $p_{\infty}$ depends only on the direction vector $(l, m, n)$ and the focal length $f$ . It does not depend on the starting points $A_{0}$ or $B_{0}$ .

Therefore, all lines with direction $(l, m, n)$ will intersect at this specific point on the image plane. This point is Vanishing Point.

THE Projection Equation

Pasted image 20251121184552.png

λ [\begin{matrix} u \\ v \\ 1 \end{matrix}] = K [R | t] [\begin{matrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{matrix}]

or in Camera Coordinates:

λ [\begin{matrix} u \\ v \\ 1 \end{matrix}] = K [\begin{matrix} X_{c} \\ Y_{c} \\ Z_{c} \end{matrix}]

Henceforth $[R | t]$ are the Extrinsic Parameters and $K$ is the Intrinsic Matrix.

Radial Distortion

For most lens it would just be quadratic but higher order terms can be introduced:

[\begin{matrix} u_{d} \\ v_{d} \end{matrix}] = (1 + k_{1} r^{2} + k_{2} r^{4} + k_{3} r^{6}) [\begin{matrix} u - u_{0} \\ v - v_{0} \end{matrix}] + [\begin{matrix} u_{0} \\ v_{0} \end{matrix}]

Perspective Projection

The Proof: Why Parallel Lines Meet

THE Projection Equation

Radial Distortion

Camera Caliberation

Camera Resection

Epipolar Geometry