Here, P is the Projection Matrix that combines both Intrinsic and Extrinsic Parameters.
Now remember that this is homogeneous coordinates, so to get the actual pixel coordinates.
So $\lambda x=x$, so let's say you want to solve for P.

Because every $X_w⟺x_c$ we get 2 equation each for x and y component in the Image.

So, we need 6 points to solve for the 11 unknowns in P (since it's up to scale). 11 only because for eg: $P_{34}=1$, we can get away, let's do math we will reach this conclusion after writing 3-4 equations:

Dividing by $z_i$:

Rearranging:

This is in the form of $Ap=0$ where A is the matrix of coefficients and p is the vector of unknowns in P.

To solve for P, we can use Singular Value Decomposition (SVD) on matrix A. The solution for p will be the right singular vector corresponding to the smallest singular value of A. This gives us the projection matrix P up to a scale factor.

So, with 6 points we can solve for P.

For more than 6 points:

• Overdetermined set of equations.
• We have to be careful as to avoid the trivial solution of $P=0$
• If observations are noisy we are cooked, P might not exist.

NOTE! -- Cautionary Tale:

• We also don't have solution if all points are coplanar. ( i.e. Z is constant for all points )
• All points lying on a line is even worse.
• All points and projection center located on a twisted cubic curve.

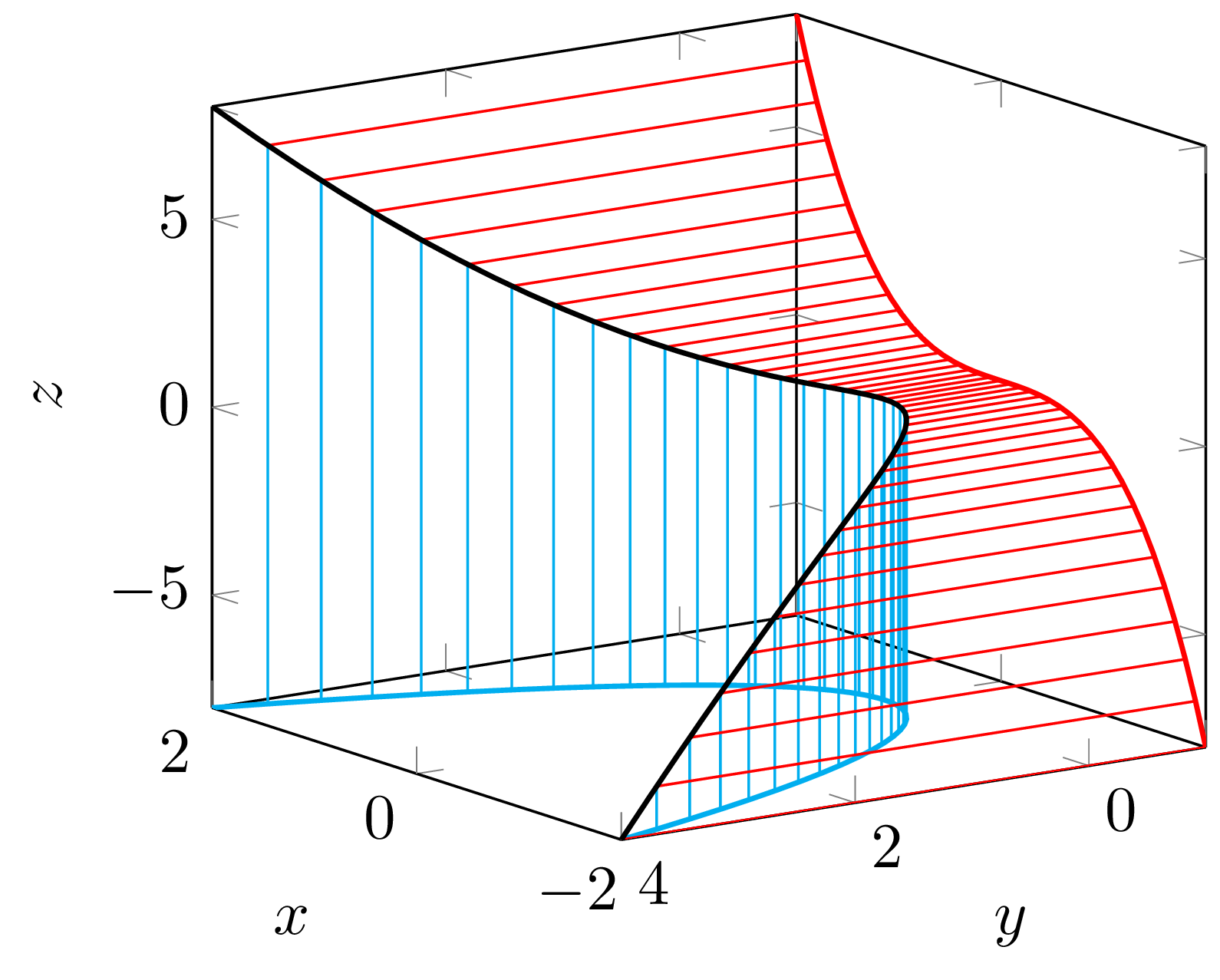
We have the system $A_{(2M\times 12)}p=0$.
In reality, due to noise, $Ap\ne 0$. We want to find $\mathbf{p}$ that minimizes the error $\parallel A\mathbf{p}\parallel$.

If we just minimize $\parallel A\mathbf{p}\parallel$, the math gives us the trivial solution $\mathbf{p}=0$ (a vector of all zeros), which is physically meaningless.
To fix the scale and avoid the zero vector, we add a constraint:

Now the problem is:
Minimize $\parallel Ap{\parallel }^2$ subject to $\parallel p{\parallel }^2=1$.

using Lagrange Multipliers. Define the loss function $L$:

Take the derivative w.r.t $\mathbf{p}$ and set to 0:

This is the definition of an Eigenvalue Problem:

1. $p$ must be an eigenvector of the matrix $A^{T}A$.
2. $\lambda$ is the corresponding eigenvalue.

Which eigenvector? Substitute back into the error equation:

To minimize the error, we must choose the smallest eigenvalue ${\lambda }_{min}$.
Thus, the solution $\mathbf{p}$ is the eigenvector of $A^{T}A$ corresponding to the smallest eigenvalue.

The SVD Soln:
Calculating $A^{T}A$ is numerically unstable (squares the condition number). So we just SVD on A.

The columns of $V$ (rows of $V^T$) are the eigenvectors of $A^{T}A$.
The singular values $\sigma$ are the square roots of eigenvalues $\lambda$.

Therefore, the eigenvector for the smallest eigenvalue corresponds to the smallest singular value. In standard SVD implementations, values are sorted high-to-low, so this is the last column of V (or last row of $V^T$).

V is 12 x 12, so the last column of V gives us the solution for P (up to scale). ( It's 12 x 12 because A is 2M x 12, so V is always 12 x 12).

After solving the DLT system $Ap=0$ using SVD, we recover P (up to scale).

Getting K from P:

import numpy as np
from scipy.linalg import rq


def decompose_projection_matrix(P):
    """
    Decomposes P = K [R | t] using RQ decomposition.

    Args:
        P: 3x4 Projection Matrix

    Returns:
        K: 3x3 Intrinsic Matrix
        R: 3x3 Rotation Matrix
        t: 3x1 Translation Vector
        C: 3x1 Camera Center in World Coordinates
    """
    # 1. Split P into M (3x3) and p4 (3x1)
    M = P[:, 0:3]
    p4 = P[:, 3]

    # 2. RQ Decomposition of M
    # scipy.linalg.rq returns K, R such that M = K @ R
    # K is upper triangular, R is orthogonal
    K, R = rq(M)

    # 3. Fix Signs (Enforce positive diagonal for K)
    # The decomposition is not unique. We need K[i,i] > 0.
    # If K[i,i] < 0, we negate the i-th column of K and i-th row of R.
    T = np.diag(np.sign(np.diag(K)))

    K = K @ T
    R = T @ R

    # 4. Enforce det(R) = 1 (Proper Rotation)
    # If det(R) = -1, it's a reflection. Negate the whole matrix?
    # Actually, standard RQ usually handles this, but strictly:
    # If det(R) < 0, we might have a coordinate system flip.
    # Usually scaling P by -1 fixes this if P was homogeneous.

    # Normalize K so K[2,2] = 1
    K = K / K[2, 2]

    # 5. Recover Translation t
    # p4 = K @ t  =>  t = inv(K) @ p4
    t = np.linalg.inv(K) @ p4

    # 6. Recover Camera Center C
    # C = -inv(M) @ p4
    C = -np.linalg.inv(M) @ p4

    return K, R, t, C


if __name__ == "__main__":
    # Ground Truth
    K_true = np.array([[1000, 0, 320], [0, 1000, 240], [0, 0, 1]])
    # Rotation 90 deg around Z
    R_true = np.array([[0, -1, 0], [1, 0, 0], [0, 0, 1]])
    # Translation
    t_true = np.array([10, 20, 5])

    # Construct P
    P_true = K_true @ np.column_stack((R_true, t_true))

    print("Ground Truth P:\n", P_true)

    # Decompose
    K_est, R_est, t_est, C_est = decompose_projection_matrix(P_true)

    print("Estimated Parameters")
    print("K:\n", np.round(K_est, 2))
    print("R:\n", np.round(R_est, 2))
    print("t:", np.round(t_est, 2))
    print("Camera Center C:", np.round(C_est, 2))

    # Sanity Check: Does K[R|t] reconstruct P?
    P_reconst = K_est @ np.column_stack((R_est, t_est))
    print("\nReconstructed P:\n", np.round(P_reconst, 2))

Calibration using Checkerboards ( Zhang's Method )

1. Detect corners in the checkerboard images to get image points.
2. The corner of the checkerboard is set to be the origin in the world frame. Also assuming that checkerboard is on the plane Z = 0 of the world frame, i.e., all points on the checkerboard have Z = 0.

So, we can remove the 3rd column of R as Z = 0 in world coordinates.

This is a homography transformation from world points on the checkerboard plane to image points.

So our long 2 x 12 matrix A reduces to a 2 x 9 matrix for each image by putting Z = 0. Which looks like:

With M points in the checkerboard, we get a 2M x 9 matrix A. We can solve for H using SVD as before.
Since H only has 8 unknowns (up to scale), we need at least 4 points (8 equations) to solve for H.
With multiple images of the checkerboard taken from different angles, we can compute multiple homography matrices $H_1,H_2,\dots ,H_n$.
From each homography H, we can extract constraints on the intrinsic matrix K.

Extracting K from multiple Homographies

From the homography, we have:

Rearranging:

Since $r_1$ and $r_2$ are orthogonal unit vectors (columns of a rotation matrix), we have the following constraints:
Because $r_1^T{r}_2=0$ ->

Because $||r_1||=||r_2||=1$ ->

Let $B=K^{-T}{K}^{-1}$, which is symmetric. We can express B in terms of the intrinsic parameters:

We can run Cholesky decomposition on $B^{-1}$ to get K by writing it as:

which follows the chol(A) = L where $A=L{L}^T$. Here $L=K^{-T}$.

Since B is symmetric, we only have to solve for 6 unique elements in B.

Defining a vector $b=[B_{11},B_{12},B_{22},B_{13},B_{23},B_{33}{]}^T$.

We have $H^{T}BH=0$ and $H^{T}BH-H^{T}BH=0$.
So we have to derive the equations in terms of the elements of b. Getting the G matrix such that $Gb=0$.
From the first constraint:

Expanding this gives:

This can be written in the form:

o, G becomes:

In general for i,j:

From the second equation of Homograph constraints:

So we can stack these equations for multiple images to form a matrix G such that:

With n images, we have 2n equations. To solve for the 6 unknowns in b, we need at least 3 images (6 equations).

To solve this we will do SVD on G:

Soln: Last column of V gives us b.

Which gives us our B matrix. From B we can get K using Cholesky decomposition as mentioned before.

Requirement to get K:

• At least 3 images of the checkerboard from different angles.
• At least 4 points in each image to compute Homography. ( 8 equations for 8 unknowns in H )
• Detect corners accurately in the images to get precise image points.

Original Zhang:

import numpy as np


def get_v_ij(H, i, j):
    """
    Calculates v_ij vector (1x6) from columns i and j of Homography H.
    Indices i, j are 0-based (0, 1, 2 correspond to 1, 2, 3 in math).
    Equation: v_ij = [h1i*h1j, h1i*h2j + h2i*h1j, h2i*h2j,
                      h3i*h1j + h1i*h3j, h3i*h2j + h2i*h3j, h3i*h3j]
    """
    h_i = H[:, i]
    h_j = H[:, j]

    v = np.array(
        [
            h_i[0] * h_j[0],
            h_i[0] * h_j[1] + h_i[1] * h_j[0],
            h_i[1] * h_j[1],
            h_i[2] * h_j[0] + h_i[0] * h_j[2],
            h_i[2] * h_j[1] + h_i[1] * h_j[2],
            h_i[2] * h_j[2],
        ]
    )
    return v


def solve_intrinsic_matrix(homographies):
    """
    Solves for K given a list of Homography matrices (at least 3).
    Uses Zhang's constraints to solve Gb = 0.
    """
    # 1. Build Matrix G (2N x 6)
    G = []
    for H in homographies:
        # Constraint 1: h1^T B h2 = 0  =>  v12^T b = 0
        v12 = get_v_ij(H, 0, 1)

        # Constraint 2: h1^T B h1 - h2^T B h2 = 0  =>  (v11 - v22)^T b = 0
        v11 = get_v_ij(H, 0, 0)
        v22 = get_v_ij(H, 1, 1)
        v_diff = v11 - v22

        G.append(v12)
        G.append(v_diff)

    G = np.array(G)

    # 2. Solve Gb = 0 using SVD
    # b is the eigenvector corresponding to smallest eigenvalue
    U, S, Vt = np.linalg.svd(G)
    b = Vt[-1]

    # 3. Reconstruct B matrix
    # b = [B11, B12, B22, B13, B23, B33]
    B = np.array([[b[0], b[1], b[3]], [b[1], b[2], b[4]], [b[3], b[4], b[5]]])

    # Check if B is positive definite. If not, flip sign of b (scale ambiguity).
    # B must be positive definite for Cholesky.
    # Simple check: B[0,0] should be positive (related to 1/fx^2)
    if B[0, 0] < 0:
        B = -B

    # 4. Cholesky Decomposition: B = L L^T
    try:
        L = np.linalg.cholesky(B)
    except np.linalg.LinAlgError:
        print(
            "Error: B is not positive definite. Data too noisy or singular configuration."
        )
        return np.eye(3)

    # 5. Compute K
    # B = (K^-1)^T (K^-1) = L L^T  =>  L = (K^-1)^T  =>  L^T = K^-1
    # K = inv(L^T)
    K_inv = L.T
    K = np.linalg.inv(K_inv)

    # Normalize K so K[2,2] = 1
    K = K / K[2, 2]

    return K


if __name__ == "__main__":
    # Ground Truth K
    K_true = np.array([[1000, 0, 320], [0, 1000, 240], [0, 0, 1]])

    # Generate random rotations/translations to make fake Homographies
    H_list = []
    for i in range(3):
        # Random rotation (using small angles for simplicity)
        ang = np.random.rand(3) * 0.5
        from scipy.spatial.transform import Rotation

        R = Rotation.from_euler("xyz", ang).as_matrix()
        t = np.random.rand(3, 1)

        # H = K [r1, r2, t]
        # We remove the 3rd column of R (Z-axis)
        H_sim = K_true @ np.hstack((R[:, [0, 1]], t))
        H_sim = H_sim / H_sim[2, 2]  # Normalize
        H_list.append(H_sim)

    # Solve
    K_est = solve_intrinsic_matrix(H_list)

    print("True K:\n", K_true)
    print("\nEstimated K:\n", np.round(K_est, 2))